
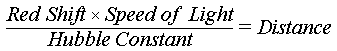
You will make several measurements of the radius of the Einstein ring and average them to reduce random scatter. The result: a ring of light from the source, centered on the lens. If the source, lens, and observer are perfectly aligned, this will occur for every ray that leaves the source at the same angle. In that diagram, a light ray leaves the source, is bent in the lens plane, and reaches the observer. The simulated image in the lower-left corner shows an idealized Einstein ring surrounding a point like "lens" (source of gravity that bends the light making up the ring. Finally, you will use the results of the first two steps to calculate the mass of the lensing object, using the Lens Mass Calculator (the third interactive element).

This will make use of the Redshift Calculator (the second interactive element below). Next, you will determine the distances of the light source and the lensing object, based on each object's redshift as well as some numbers that describe our universe's expansion. First, you will measure the radius of a simulated Einstein ring, using the Einstein Ring Simulation (the first of three interactive elements below). You will carry out the lab in three steps. 1.37 Lens Mass (M.) 1.83e+12 CalculateĪssessment: Weighing a Gravitational Lens The simulation below will help you study gravitational lensing by modeling the formation of an Einstein ring. Enter the values for lens distance in parsecs, source distance in parsecs, Einstein angle in arcseconds, and press the Calculate button. Instructions Calculate the Lens Mass 2.977e9 Lens Distance (pc): Source Distance (pc): Einstein angle ("): 4.761e9 This is a calculator for the Lens Mass. For example, if this number is 0.14, the light was emitted when the Universe was only 14 percent of its present age (with the age depending on the input Hubble and declaration parameters). The bottom field gives the lookback time as a fraction of the age of the Universe when the light was emitted. 65 Deceleration parameter a 0.5 Calculate 8.960e-1 Velocity (v/c) Distance (ly) Distance (pc) Look-back time (yr) Fractional age of the Universe when emitted 1.552e+10 4.761e+9 8.890e+9 1.133e-1 The relativistic formula is used to approximately relate vlc (velocity divided by the speed of light) to the redshift z. Press the Calculate button to calculate the lookback times, the distances, and the fractional age of the Universe when emitted. Use the sliders to set the values for the redshift z, the Hubble parameter H 0, and the deceleration parameter q. Instructions Redshift z 3.27 Hubble parameter Ho (km/s/Mpc) This calculator allows to calculate the lookback times, the distances, and the recessional velocities for the specific values of the redshift z, the Hubble parameter H 0, and the deceleration parameter q. Record this larger Distance (pc) value in the Source Distance (pc) box of the Lens Mass Calculator. Repeat Steps 1-4, but with the larger z value from the simulator. Write it down as well, you will need it for a question below. Record the Distance (pc) value in the Lens Distance (pc) box of the Lens Mass Calculator. Set the Deceleration parameter to 0.5 (ditto). Set the Hubble parameter to 65 (this value may already be displayed, in which case no adjustment is needed). Set Redshift z to the smaller z value from the simulator, either by using the slider or by typing it into the entry box. Transcribed image text: 2) Distance Assessment (Redshift Calculator) 1.


 0 kommentar(er)
0 kommentar(er)
